Maths of music
Music is ruled by mathematical laws. Staring at the numbers was not enough for me though, so I have coded a tool to actually listen to it.
Music theory goes interactive
The widget can take up to one minute to load, so in the meantime let me explain what you can do with it.
The main concept the tool revolves around is that of musical scale, i.e., a set of musical notes ordered by their pitches. This definition is almost valid for chords as well, with the subtle difference that chord notes are meant to be played simultaneously while the notes of a scale are not.
While exploring different scales and chords you can also tune these additional parameters:
- Number of notes: You may only be familiar with scales that have 7 notes (a.k.a the diatonic scale, C-D-E-F-G-A-B, Do-Re-Mi-Fa-Sol-La-Si or the white keys of the piano) or 12 notes (the chromatic scale, if we add the black keys as well), but from 1 to 53 and beyond all qualify as musical scales, and you are free to to select many of them.
- Tonic: This is the first note in the scale, which you can also select. In the case of chords (and forgetting about chord inversions), the first note is called the root of the chord.
- Tuning: Note pitches and intervals have not remained the same across centuries and cultures. From ancient Greece over the Baroque period up to our days, you can take a listen how tuning the old good scales was in the old good days. The different tuning options are explained below.
The resulting encircled starry diagram shows how notes in the scale are distributed and where they come from. For further customization you can just modify the interval of the individual notes with respect to the root. The number right to the corresponding slider will show the modified pitch in cents.
Once you have pimped up your scale you can listen to the result1. For a number of notes of 4 or less you will also hear them simultaneously at the end, implying the corresponding chord.
That is pretty much it. The rest of this page is just my humble attempt to explain the music theory you need to know to fully understand the widget, as well as the mathematics and physics beneath. Needless to say, there are much better resources out there, so if you can spare 5-10 minutes I really encourage you to check some of the videos I have used as a reference.
What makes sound harmonious?
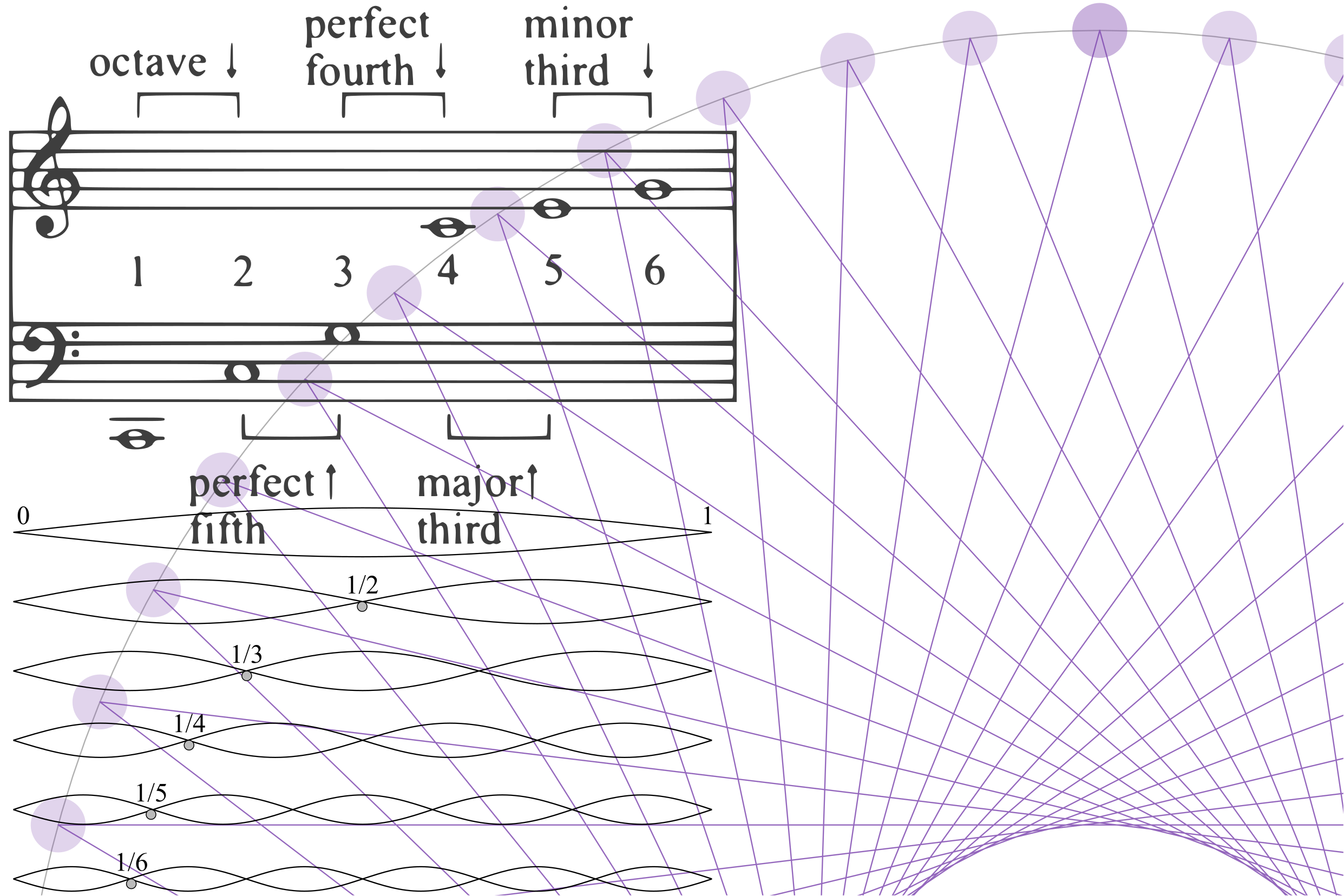
Humans find two notes pleasant or consonant when their pitches form a simple ratio. Here is a list of the most common examples of harmonious intervals and their frequency ratios:
| Interval | Example notes | Frequency ratio |
|---|---|---|
| Octave | C-C’ | 1:2 |
| Fifth | C-G | 2:3 |
| Fourth | C-F | 3:4 |
| Major third | C-E | 4:5 |
| Minor third | A-C | 5:6 |
On the other hand, irrational relations such as \(1:\sqrt{2}\) (whose simplest good rational approximation is \(32:45\)) sound cacophonous or dissonant to our ears. In the case of \(1:\sqrt{2}\), by the way, we are talking about the infamous tritone, also known as diminished fifth or diabolus in musica. This interval, which is found between F and B in the diatonic scale, was avoided for centuries because of its spooky, dissonant sound.
The preference for simple ratios can be explained out of the physics of strings and air vibrations, which account for the way how most instruments (including the human voice) produce notes. In a nutshell, vibrating strings (same as vibrating air inside of a tube) are restricted to generate sound waves at frequencies which are a multiple of a fundamental frequency. These sound waves, known as partials, resonate all at once whenever the string vibrates, and the underlying fundamental frequency is what we perceive as the note’s pitch.

The simpler the relation between two notes is (as in the table above), the more partials both notes will have in common and the more pleasant they will sound when played together.
How do we build a scale?
Now that we know which notes sound good together, we can ask ourselves which ones we should use to play a melody. In other words, which notes we should use to build a scale.
For that we can start by choosing notes whose frequency ratios are as simple as possible. As already mentioned, the simplest ratio equals 1 to 2 and corresponds to the octave. However, that ratio is so simple that humans universally perceive it as the same note, but played at different pitches.
Also because of this, we can arbitrarily pick a first note and then restrict our search to notes whose pitch is 1 to 2 times that of our first note. The reason for this is that any other pitch out of this range can be multiplied or divided by 2 as many times as needed until its ratio to the first note falls under the interval \(\left(1,2\right)\), and it will still be perceived as the same note, just in a different octave.
This leads to a periodic structure that repeats over and over again every time we jump into the next octave. In the widget graph, this periodicty is represented by the circle. One turn around it equals one octave, and if we for instance traverse one octave and a half on the graph we will end up only half an octave away from the starting point.
Once that we have ruled out the octave, the next simplest interval is the fifth at \(2:3\). With that we can already find new notes, e.g. if we start with a frequency of 100 Hz and we focus on pitches between 100 and 200 Hz:
\[\begin{aligned} f_1 &= 100\textrm{ Hz} \\ f_2 &= \frac{3}{2}\cdot 100 = 150\textrm{ Hz} \end{aligned}\]Here \(f_2\) is the fifth of \(f_1\). We can further calculate the fifth of \(f_2\):
\[f_3 = \frac{3}{2}\cdot 150 \cdot\frac{1}{2} = 225 \cdot\frac{1}{2} = 112.5\textrm{ Hz}\]225 Hz is already greater than 200 Hz, hence the division by two to find the note in a lower octave as 112.5 Hz. If we keep multiplying by \(\frac{3}{2}\) and fitting to the octave \(\left(100,200\right)\) we will always encounter a new note. That is how many scales in the widget are generated2.

The purple connecting lines in the widget graph above represent the fifth intervals that generate these scales2. The resultant star patterns are the basis of the so-called theory of well-formed scales.
The theory of well-formed scales gives a mathematical answer to the following question: how did different musical cultures fix the number of notes they use in their scales? This can be broken down to more specific questions, for instance:
- Why does the Western diatonic scale have 7 notes?
- Why is the diatonic scale extended into a 12-note chromatic scale?
- Why is the pentatonic scale so prevalent in so many cultures, most notably in East Asia?
- Why did Arabic musicians latch onto the 17-tone scale before moving on to the quarter-tone scale with 24 steps?
All this scales can be derived from successive fifths. What makes numbers 5, 7, 12 or 17 special is that, for those scales, a note and its fifth are always separated by the same number of notes. The same goes for 53-tone scales as studied by Chinese theorists. This is the property that makes a scale well-formed. Even the name fifth comes from this: To find the fifth of a certain note in a diatonic scale, all you have to do is to count up to five through the notes of the scale starting by your reference note.
In the widget, you can check visually whether a scale is well-formed if you choose the tuning as “Equally divided octave”. The resulting diagrams form regular stars for a number of notes of 3, 5, 7, 12, 17 and 53. This is a graphical confirmation of their “wellformedness”, and it contrasts with non-well-formed 4-note, 6-note or 24-note scales.
How do we tune our scales?
By now it should be clear that we can build a scale from two fundamental consonant intervals: octaves and fifths. Furthermore, we have assumed a ratio of \(\frac{2}{1}\) for octaves and \(\frac{3}{2}\) for fifths because of their pure, harmonious sound. This setup is simple, easy to understand and it has been massively used throughout history. In Europe, we have Greek mathematician Pythagoras as one of the earliest developers of this method, up to the point that the tuning of the resulting notes is referred to as Pythagorean tuning.
Pythagorean tuning based on pure fifths presents, however, two major problems:
- While it preserves octaves, fifths and fourths perfectly harmonious, other intervals today considered as consonant deviate significantly from their ideal ratio. Major thirds, for instance, are the next consonant interval with a ratio of \(\frac{5}{4}=1.25\). Nevertheless, Pythagorean tuning assigns \(\frac{81}{64}=1.265625\) to them, which constitutes a difference of 21.51 cents or an audible relative pitch error of 1.25%3.
- When stacking fifths up to the 12-note chromatic scale, the last added note does not form a perfect fifth with the initial note (A# to F in the animation above), but a narrowed version with a difference of around 23 cents or 1.3% relative pitch error. This interval is perceptively dissonant and it is known as the wolf fifth because of its howling sound.
We can try to change our fundamental intervals to compensate for that. The octave ratio of \(1:2\) is rarely altered though, as it constitutes a universal pillar of music perception, so we will have to tweak or temper our fifth to slightly different values. This concept of building a scale for different fifth ratios leads to the so-called regular temperaments. The ones I have considered in the widget are the following ones:
| Temperament | Fifth ratio | Fifth cents | Observations |
|---|---|---|---|
| Pythagorean | \(\frac{3}{2}=1.5\) | 702 | This is the temperament I just explained above, which generates pure fifths and fourths. |
| (1/4-comma) Meantone | \(\sqrt[4]{5}=1.4953\ldots\) | 697 | Most prominently used in the Renaissance and Baroque periods, this temperament narrows the fifth to achieve pure major thirds and minor sixths at \(\frac{5}{4}\) and \(\frac{8}{5}\), respectively. |
| Equal temperament | \(2^{\frac{7}{12}}=1.4983\ldots\) | 700 | 12-tone equal temperament is the tuning system used by most music pieces nowadays. It exhibits a slightly narrow fifth to generate equally spaced notes in the chromatic scale, eliminating wolf intervals. |
Same as for the 12-tone equal temperament, one could adjust the fifth interval to achieve regularly spaced notes for any arbitrary number of notes. This option is selectable in the widget as “Equally divided octave” and it is generally as visually pleasing as acoustically unsettling, so use it at your own risk.
In contrast with all these tuning systems, just intonation tuning does not stick to a fixed-size fifth but it rather adjusts every individual note to form a pure interval with the tonic note. The drawback of this system is its inflexibility; tunes based on the reference note will sound great, while other keys will not sound as harmonious or they will be directly cacophonous.
In the widget, C has been taken as the reference note for just intonation in order to explore which keys work with it and which ones do not. You can, for instance, check the howling sound of its F#-C# fifth, which does not appear in equal temperament. Similarly, the wolf interval of Pythagorean and meantone tuning has also been placed between F# and C# for consistency.
In the table below you can check the just intervals I have used as a reference, as well as its comparison with the available regular temperaments. As a rule of thumb, a difference equal or greater than \(\pm 10\) cents can be noticed by most people (you can read more about cents and human perception below).
| Note | Interval from C | Just intonation ratio | Deviation from equal temperament | Deviation from Pythagorean tuning | Deviation from 1/4-comma meantone temperament |
|---|---|---|---|---|---|
| C | Unison | 1:1 | 0 cents (0.00%) |
0 cents (0.00%) |
0 cents (0.00%) |
| C# | Minor second | 15:16 | -12 cents (-0.70%) |
-22 cents (-1.27%) |
+5 cents (+0.29%) |
| D | Major second | 8:9 | -4 cents (-0.24%) |
0 cents (0.00%) |
-11 cents (-0.64%) |
| D# | Minor third | 5:6 | -16 cents (-0.92%) |
-22 cents (-1.27%) |
-6 cents (-0.35%) |
| E | Major third | 4:5 | +14 cents (+0.82%) |
+22 cents (+1.28%) |
0 cents (0.00%) |
| F | Perfect fourth | 3:4 | +2 cents (+0.12%) |
0 cents (0.00%) |
+5 cents (+0.29%) |
| F# | Tritone | 32:45 | +10 cents (+0.58%) |
+22 cents (+1.28%) |
-11 cents (-0.64%) |
| G | Perfect fifth | 2:3 | -2 cents (-0.12%) |
0 cents (0.00%) |
-5 cents (-0.29%) |
| G# | Minor sixth | 5:8 | -14 cents (-0.81%) |
-22 cents (-1.27%) |
0 cents (0.00%) |
| A | Major sixth | 3:5 | +16 cents (+0.93%) |
+22 cents (+1.28%) |
+6 cents (+0.35%) |
| A# | Minor seventh | 5:9 | -18 cents (-1.04%) |
-22 cents (-1.27%) |
-11 cents (-0.64%) |
| B | Major seventh | 8:15 | +12 cents (+0.70%) |
+22 cents (+1.28%) |
-5 cents (-0.29%) |
| C’ | Octave | 1:2 | 0 cents (0.00%) |
0 cents (0.00%) |
0 cents (0.00%) |
Let me suggest a couple of experiments you can try with the widget to explore different temperaments:
- Check the sound of wolf fifths. Select number of notes 2, root F# and scale fifth. Listen to it for different tunings: you should find it consonant for equal temperament and dissonant otherwise.
- Check the “impurity” of thirds in equal temperament. Select number of notes 2, root C and scale major third. The sound should ring out pure for just intonation and meantone tuning. When playing both notes together in equal temperament, however, you may notice a subtle wobbling effect (kind of a rapid wah-wah-wah vibration) that you did not hear before. This is how “impure” thirds are in the music we listen to every day, even though we do not pay attention to it.
- You can repeat the same experiment for minor thirds. These ring out nice and smooth for just intonation and wobble to a certain extent otherwise.
Cents or the human perception of music
Music intervals are formally studied using a measure unit called cent. The reason for using cents instead of a more physic-related unit of frequency such as hertz or cycles per second has to due with our own perception of sound. Pitch is perceived logarithmically, meaning that we feel two notes vibrating at 100 and 200 cycles per second as far apart as if they were vibrating at 200 and 400 cycles per second, or 400 and 800, etc. It is not the frequency difference that matters, but the frequency ratio; the ratio in the just mentioned examples stays constant at \(1:2\) (which you can recognize as the octave interval). This is what we refer to with logarithmic phenomenon.
The cent is a logarithmic unit of pitch that allows us to reason about music perception in a much simpler way. 1 cent equals the 100th part of an equal-tempered semitone, 100 cents equal one semitone, 200 cents equal a whole tone, and since one octave comprises 12 semitones we can go on until we get 1200 cents = 1 octave.
Cents have also allowed scientists and musicians to investigate and measure the limits of human music perception. It may be useful just to drop a couple of illustrative figures4, as cents are extensively discussed above:
| Pitch ratio in cents | Relative difference in linear frequency | Human perception |
|---|---|---|
| 1 cent | \(<0.06\%\) | Unnoticeable. |
| 5 cents | \(<0.3\%\) | Just noticeable for trained ears. |
| 10 cents | \(<0.6\%\) | Generally noticeable when two notes played together. |
| 20 cents | \(<1.2\%\) | Generally noticeable when two notes played successively. |
| 50 cents | \(<3\%\) | Quarter tone interval. Rarely used in Western music, highly important in Middle Eastern music. |
| 100 cents | \(<6\%\) | Semitone interval. Definitely noticeable if familiar with Western music. |
Fascinating enough, this reveals that our ability to discriminate pitch goes below a relative error of 0.6%, and that a semitone interval, with all its prevalence in Western music, accounts for less than 6% increase in frequency.
References
YouTube
Note My personal recommendation is to go for the Lemnismath video if you understand Spanish, as it covers the basics for overtones and intervals plus the theory of well-formed scales. Unfortunately I have not found any good reference for the said theory in English, but Minute Physics video does a superb job summarizing everything else in less than 5 minutes.
Papers
- N. Carey and D. Clampitt, “Aspects of Well-Formed Scales,” Music Theory Spectr, vol. 11, no. 2, pp. 187–206, Oct. 1989, doi: 10.2307/745935.
- M. Castrillón and M. Domínguez, “Un encuentro entre las matemáticas y la teoría de escalas musicales: Escalas bien formadas,” La Gaceta de la RSME, vol. 16, no. 1, pp. 87–106, 2013.
-
I have actually coded the note generation process from scratch, as I wanted to have harmonic-rich synth-like sounds that I can arbitrarily fix to any frequency. ↩
-
The stacking fifth method is used to build all modal, major or minor scales. In other cases (blues scale, harmonic minor, intervals and chords) the purple lines just involve some abuse of notation. Sorry not sorry. ↩ ↩2
-
Greeks actually deemed thirds dissonant for this reason. ↩
-
Although one might extract a linear relation between cents and frequency relative error from the table, this is just a linear approximation for small quantities. ↩